Kalachand Sain
National Geophysical Research Institute, Hyderabad 500 007, India.
E-mail: postmast@csngri.ren.nic.in
Colin A. Zelt
Department of Geology and Geophysics, Rice University, Houston, TX
77251-1892, USA. E-mail: czelt@rice.edu
P.R. Reddy
National Geophysical Research Institute, Hyderabad 500 007, India.
This paper demonstrates the effectiveness of minimum-parameter inversion to obtain the "geological" model, and minimum-structure tomography to objectively determine model resolution, error, and the structure required by the data. First-arrival seismic traveltime tomography is used to assess geologically-constrained 2-D velocity models obtained from refraction/wide-angle reflection traveltime data. The inverse approach is subjective since it involves prior geological constraints incorporated into the model using the minimum number of velocity and interface nodes. This yields a final model consistent with the seismic data as well as known geological features, such as faults. The tomographic approach objectively seeks a minimum-structure model according to the form of regularisation, the free parameter values, and an objectively-determined starting model. The tomographic approach is applied to wide-angle data recorded along the Hirapur-Mandla profile in central India across the Narmada-Son lineament (NSL) and the results are compared with a previous minimum-parameter, geologically-constrained inversion. The geological model contains a high velocity (> 6.5 km/s) anomaly beneath the NSL at a depth of ~1.5 km flanked by lower velocity (~5.3 km/s) in the fault-bounded Vindhyan basin to the northwest and ~5.9-6.0 km/s in the granitic basement to the southeast in a region masked by the basaltic Deccan Traps. For these data, the objective model demonstrates that the large-scale features of the geological model are required by the data. The tomographic approach is also used to provide estimates of model bounds and lateral resolution that would be more difficult to obtain using a minimum-parameter approach. Exploiting the complimentary nature of minimum-parameter and minimum-structure approaches for modelling and model assessment appears to be an effective strategy for the analysis of wide-angle data.

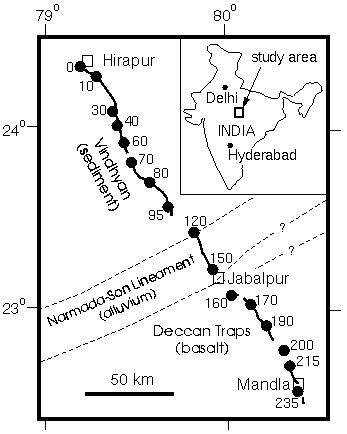
Figure 1. Location of the Hirapur-Mandla seismic profile across the Narmada-Son lineament, the northern and southern boundary of which are indicated by dashed lines. Inset shows location of study area in central India. Shot point locations indicated by solid circles and numbered according to their approximate distances (km) along the profile from the town of Hirapur in the north to Mandla in the south. Receivers were located along the black lines between the shots at a nominal spacing of 200 m.
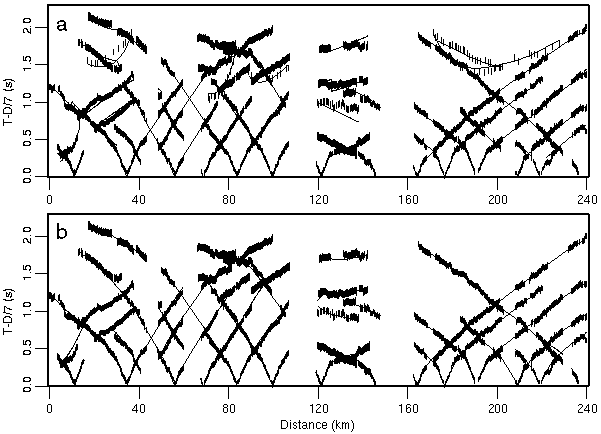
Figure 2. Comparison of observed (vertical bars) and calculated (lines) traveltimes for each shot for the (a) minimum-parameter model, and (b) preferred minimum-structure model. Length of vertical bars corresponds to pick uncertainty and the thicker vertical bars in (a) are reflected picks. Data are reduced using 7 km/s.
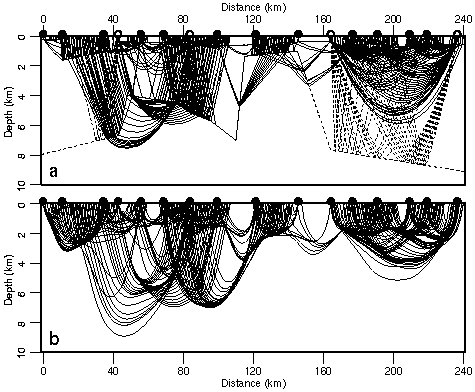
Figure 3. Ray diagrams through the final (a) minimum-parameter model, and (b) preferred minimum-structure model. For clarity, every 8th first arrival and every 2nd reflection raypath is shown. Dashed lines in (a) are layer boundaries. Shot points indicated by black dots; shots with wide-angle reflections indicated by open circles.
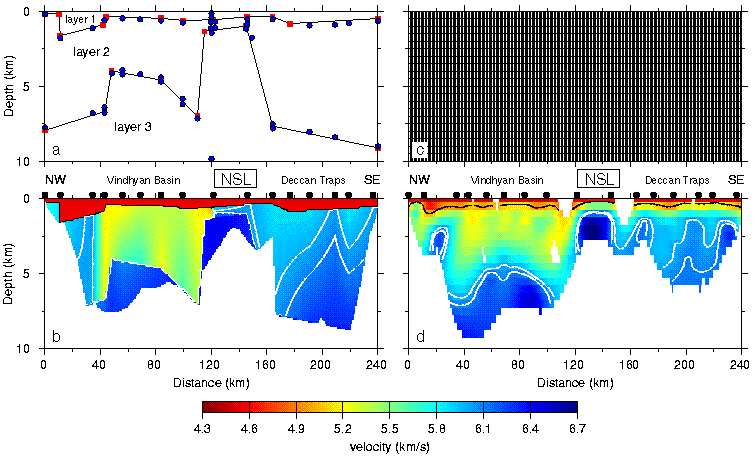
Figure 4. Comparison of parameterisations and final models for the minimum-parameter and minimum-structure approaches. (a) Velocity (blue dots) and boundary (red squares) nodes of minimum-parameter model. (b) Minimum-parameter model. (c) Constant-slowness cells of minimum-structure model; each cell is 1.0\2640.5 km in size. (d) Minimum-structure model. Black and white lines in (b) and (d) are the 5.0, 6.0 and 6.1 km/s contours. Unconstrained model regions in (b) and (d) have been omitted and black dots above models indicate shot locations. The rectangle around NSL indicates the position of the Narmada-Son lineament (Fig. 1).
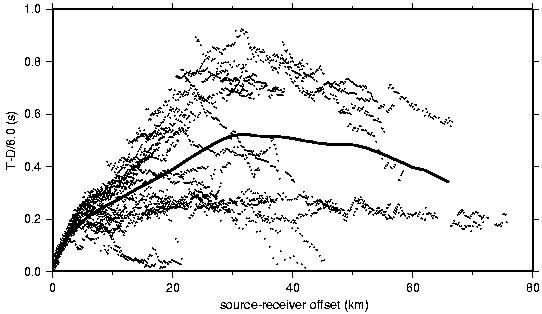
Figure 5. Complete set of 3912 first arrival picks (dots) reduced at 6.0 km/s versus source- receiver offset without regard to position along the profile. Solid line represents average time in 2- km-offset bins.
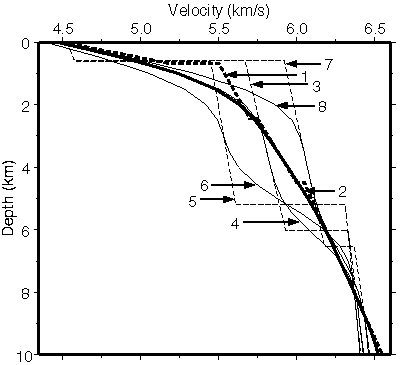
Figure 6. 1-D starting models used in the minimum-structure approach. (1) velocity-depth function derived from the average traveltimes in 2-km-offset bins (Fig. 5). (2) smoothed version of model 1. (3) velocity-depth function derived by laterally-averaging the 2-D minimum-parameter model (Fig. 4b). (4) smoothed version of model 3. (5) velocity-depth function derived by laterally- averaging the left half of the 2-D minimum-parameter model. (6) smoothed version of model 5. (7) velocity-depth function derived by laterally-averaging the right half of the 2-D minimum-parameter model. (8) smoothed version of model 7. The even-numbered starting models were smoothed using five applications of a three-point moving average filter after interpolating the odd-numbered velocity-depth functions using a 0.5 km depth interval. Model 2 is the preferred starting model.
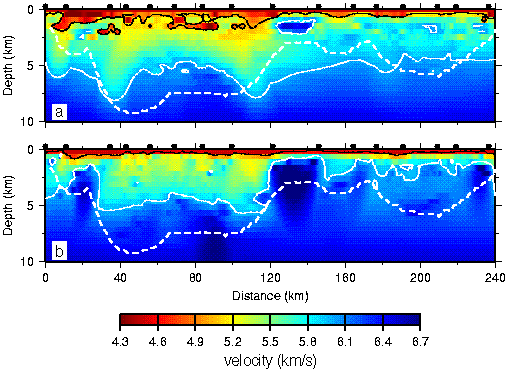
Figure 7. (a) Minimum and (b) maximum velocities at each node for the twelve models listed in Table 1 obtained using the minimum-structure approach and a range of free parameters and regularisation. The black and white lines are the 5 and 6 km/s contours. The dashed white line is the depth of penetration of raypaths in the preferred minimum-structure model (Fig. 3b). Black dots indicate shot point locations.
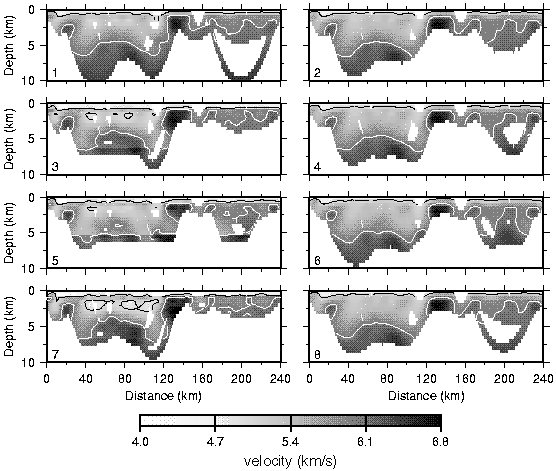
Figure 8. Final minimum-structure models corresponding to the eight 1-D starting models shown in Fig. 6. Regions not sampled by ray paths have been omitted. The black and white lines are the 5 and 6 km/s contours.
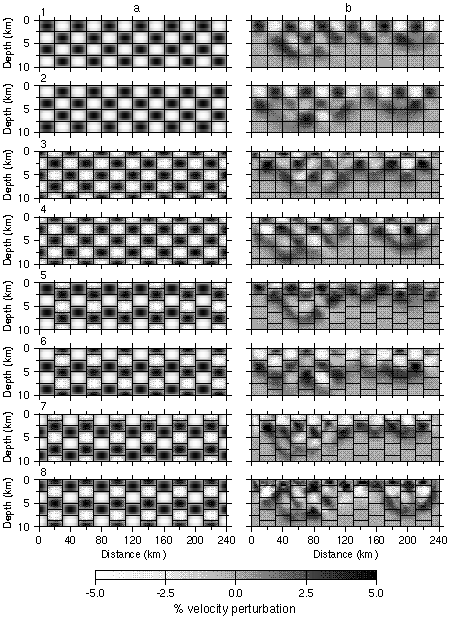
Figure 9. (a) Example of the eight types of checkerboard anomaly patterns for the 20 km cell length. (b) Corresponding recovered anomalies using the source-receiver geometry of the real data. True cell boundaries indicated by black lines.
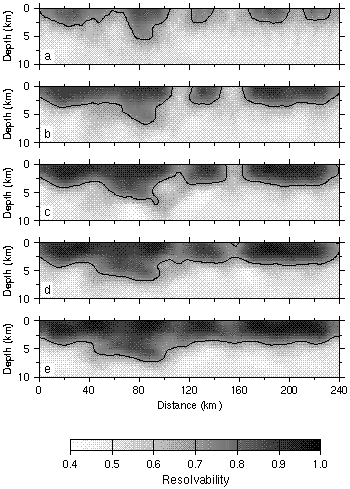
Figure 10. Average resolvabilities using the source-receiver geometry of the real data for anomaly lengths of (a) 5 km, (b) 7.5 km, (c) 10 km, (d) 15 km, and (e) 20 km. The 0.7 contour is indicated.
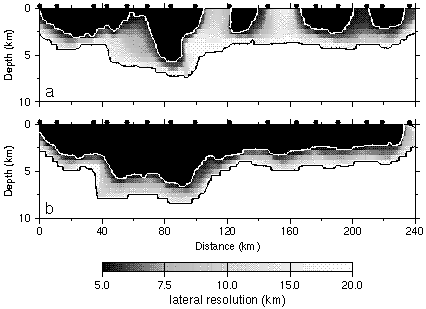
Figure 11. Lateral velocity resolution for the source-receiver geometry of the (a) real data, and (b) ideal data. See text for description of the ideal dataset. Black regions have better than 5 km lateral resolution, white regions have worse than 20 km lateral resolution. Black dots indicate shot point locations.