The crustal structure of the Omineca (OB) and Foreland (FB) belts of the southeastern Canadian Cordillera are interpreted from the inversion of seismic refraction/reflection traveltimes and amplitudes, and modeling of the Bouguer gravity data from a 350-km east-west wide-angle profile. The main features of the resultant velocity and density models include (i) a low average crustal velocity of 6.2 km/s, (ii) variable upper crustal velocities (5.6-6.3 km/s) within the FB and Purcell Anticlinorium as compared to further west in the OB (6.1-6.2 km/s), (iii) a mid-crustal ( 20 km depth) 0.4-0.5 km/s velocity increase within the OB, (iv) eastward crustal thickening from 35 to 42 km over 80 km distance beneath the OB-FB boundary, (v) the Slocan Lake fault (SLF) dipping east at 15-20 degrees to at least 35 km depth, (vi) decreased lower crustal velocities (6.7 to 6.4 km/s) across the SLF from the OB into the FB, (vii) increased uppermost mantle velocities (7.9 to 8.0 km/s) from the OB into the FB, and (viii) an average crustal density increase of 40 kg/m**3 from the OB into the FB. Lower velocities, higher conductances and increased densities within the upper crust (0-10 km depth) of the Purcell Anticlinorium appear to be associated with Middle and Upper Proterozoic rift-related metasediments and gabbroic dikes (35-55% by volume) in contrast to the mainly Mesozoic felsic intrusives and metamorphic rocks that dominate further west in the OB. Elevated crustal temperatures within the OB (a high heat flow province) are responsible for low velocity gradients to 20 km depth. A more mafic lower crust beneath the OB (inferred from higher velocities) and the westward decrease in crustal thickness are interpreted as resulting primarily from Middle and/or Late Proterozoic extension and rifting of the craton. Penetration of the SLF into the lower crust may be controlled by lateral strength contrasts at the edge of the craton. Farther west, a mid-crustal strength contrast (a velocity boundary at 20-25 km depth), may have acted as a regional detachment zone during compressional and extensional tectonic episodes.
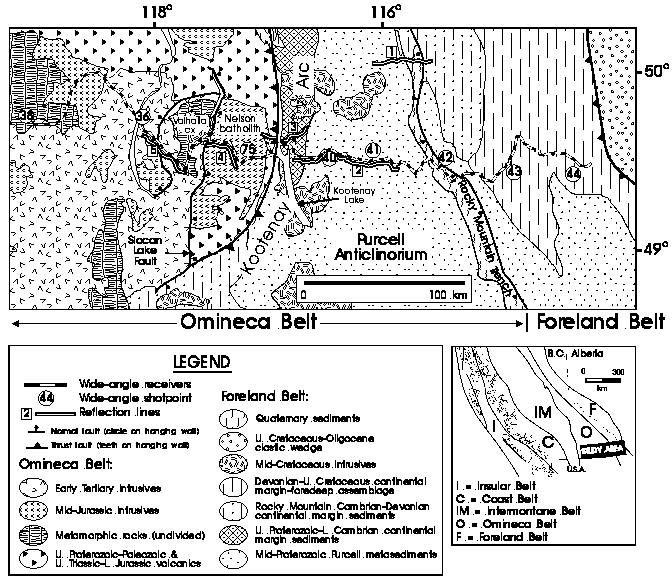
Figure 1. Location map. Shots points and receiver array of the SCoRE'90 line 9 wide-angle profile are indicated. The 1985 Lithoprobe reflection lines 1-5 are also indicated. Map at lower right shows the morphogeologic belts of the Canadian Cordillera [Monger et al., 1982] and the study area. See text for description of geological features.
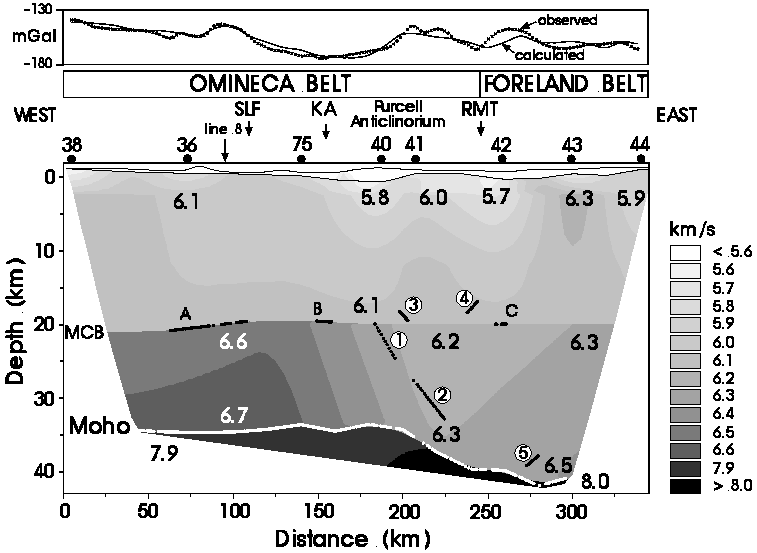
Figure 2. Final velocity model. Contoured velocity field defined by the model parameters is presented, omitting the perimeter not constrained by the wide-angle data (vertical exaggeration ~4:1). Numbers 5.7-8.0 are P-wave velocities at various positions. Upper crustal boundary at the base of the surface layer is shown and the MCB and Moho are indicated only where imaged by PcP, PmP and Pn ray paths; the three segments of PcP reflecting points are labeled A, B and C. The five floating reflectors labeled 1-5 are indicated by the reflection points corresponding to each Pr arrival. Minimal smoothing has been applied to the velocity field and layer boundaries to better represent the resolution of the wide-angle data. Shot point locations, intersection with SCoRE'90 line 8, tectonic features, and comparison of observed and calculated gravity anomalies indicated above the model; the calculated gravity values assume deviations from an empirical velocity-density relationship occur throughout the crust (see text for details). SLF = Slocan Lake fault, KA = Kootenay Arc, RMT = Rocky Mountain Trench (where crossed by the wide-angle line).
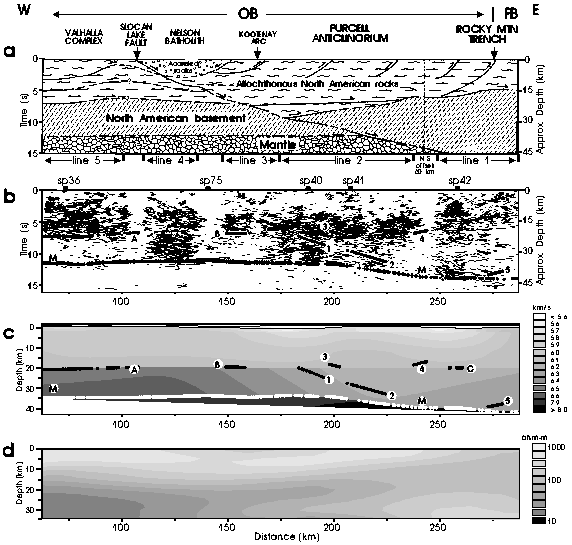
Figure 3. Comparison of Lithoprobe reflection interpretation and data, the wide-angle velocity model, and the electrical structure. (a) An interpretive section by Cook et al. [1992] of reflection lines 1-5. (b) Migrated reflection data (thin line segments) and the floating reflectors (labeled 1-5), mid-crustal boundary (A-C) and Moho (M) from the wide-angle model after converting from depth to zero-offset two-way traveltime using the velocities of the final model; dots indicate reflection points, crosses indicate head wave emergence points. The approximate depths labelled in (a) and (b) were determined assuming an average crustal velocity of 6.2 km/s. (c) Wide-angle velocity model (see Figure 2 for details). (d) Electrical structure from Jones et al. [1992]. Horizontal and vertical scales are the same for each panel; vertical exaggeration ~1:1. The reflection lines 1-5 and line 9 shots points are labeled between panel (a) and (b). See text for description of geological features and Cook et al. [1992] interpretation. OB = Omineca Belt, FB = Foreland Belt.
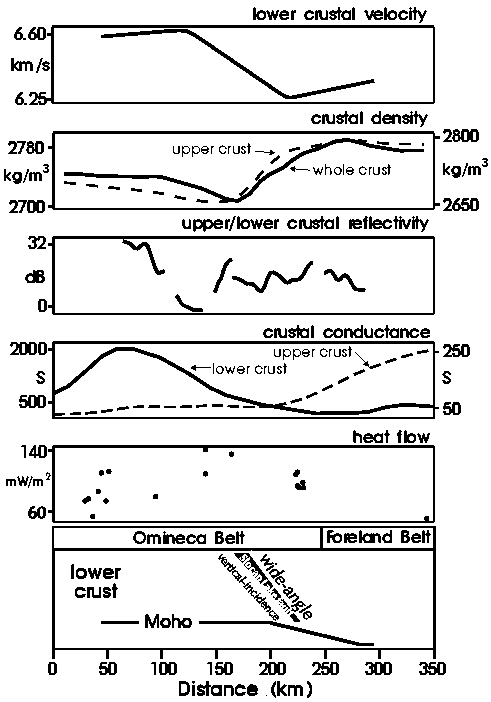
Figure 4. Comparison of geophysical data along Lithoprobe transect. The average lower-crustal velocity from the wide-angle model (top) is compared with (1) average crustal density (solid line and left scale) and average crustal density above the MCB (dashed line and right scale) obtained from modeling the regional Bouguer gravity data assuming deviations from an empirical velocity-density relationship occur throughout the crust and only above the MCB, respectively (see text for details); (2) the log of the ratio of upper- to lower-crustal coherent reflectivity from reflection lines 1-5 where coherent reflectivity equals the total length of the vertical-incidence reflection segments shown in Figure 3b calculated in 1 km bins; (3) lower-crustal conductance (solid line and left scale) and upper-crustal conductance (dashed line and right scale) from Jones et al. [1992]; and (4) heat flow values from Lewis et al. [1992], except the eastern most value is from Majorowicz and Jessop [1981]. See text for description of the geophysical data and comparisons with the wide-angle model. At the bottom of the figure the Omineca and Foreland belts are indicated along with a simplified model of the lower crust and Moho from the wide-angle model including the wide-angle image of the Slocan Lake fault and its interpreted position from the reflection data.